Función plot
Creamos un vector con las coordenadas x, en los argumentos de seq (secuencia) especificamos los límites y el número de valores intermedios o el incremento. En las coordenadas y, la función de distribución pnorm, por defecto una distribución normal estándar, N(0, 1), con una media de 0 y una varianza de 1.
x <- seq(-3, 3, 0.001) # Incremento de la secuencia: 6001 valores
# O bien
x <- seq(-3, 3, length = 1000) # 1000 valores intermedios
Usamos la función plot:
plot(x, # Coordenadas x
pnorm(x), # Coordenadas y
type = "l", # Tipo de gráfico líneas
las = 1) # Etiquetas alineadas horizontalmente
Función curve
No es necesario crear un vector con las coordinadas x. Solamente especificar el nombre de la función que evaluará: pnorm. Por defecto, curve evalua 101 valores (n = 101).
curve(pnorm(x), xlim = c(-3, 3), las = 1)
Función ecdf
La función ecdf, empirical cumulative distribution function, computa la distribución acumulada. Y plot.ecdf implementa el método plot para representarla gráficamente.
plot.ecdf(rnorm(10000)) # O más intrincadamente
plot(ecdf(rnorm(10000)))
plot.ecdf(rnorm(10000),
xlim = c(-3, 3), # Extremos del eje x
las = 1) # Etiquetas alineadas horizontalmente
Más ejemplos
Dos ejemplos con distribuciones distintas de la distribución normal estándar. En este caso, sí es necesario suministrar los argumentos media y desviación típica (raíz cuadrada de la varianza). Añadimos el parámetro xaxp para forzar el número de marcas del eje x entre las dos coordinadas de los extremos.
N(-2, 0.5)
x <- seq(-5, 5, 0.001)
plot(x, pnorm(x, -2, sqrt(.5)), type = "l", las = 1, xaxp =c(-5, 5, 10))
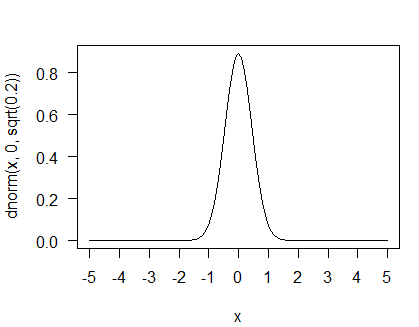
curve(pnorm(x, 0, sqrt(.2)), -5, 5, las = 1,
xaxp = c(-5, 5, 10))
























 Nube de datos
Nube de datos