Introducción al diagrama de caja (box plot) en R

El diagrama de caja —box plot— es un tipo de gráfico que utiliza los cuartiles para representar un conjunto de datos. Fue introducido por John W. Tukey en 1969. Permite observar de un vistazo la distribución de los datos y sus principales características: centralidad, dispersión, simetría y tamaño de las colas. La mejor manera de entender un diagrama de caja es gráficamente.

Explicación gráfica

Diagrama de caja - Wikipedia

Elementos y propiedades

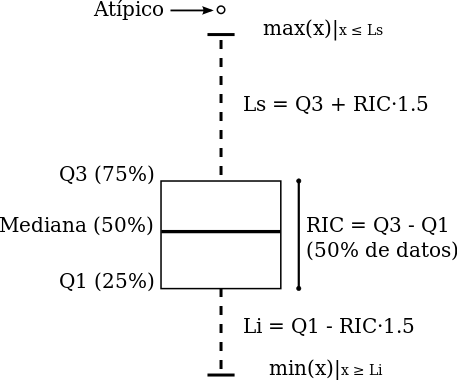
• Elementos

- Línea, dentro de la caja, es la mediana de los datos: Q2
- Caja, representa el rango intercuartílico: Q3 - Q1.
- Bigotes, las líneas sólidas al final de las líneas de guiones que se extienden desde la caja. Definen los límites más allá de los cuales consideramos los valores como atípicos. Existen diferentes modos de calcularlos D.
- Valores atípicos, aquellos puntos fuera de los bigotes. Se representan como puntos o pequeños círculos.

• Propiedades

- Centralidad y localización, representada por la mediana que es la línea que corta la caja
- Dispersión, proporcionada por la altura o longitud —si es horizontal— de la caja. También por la amplitud de los bigotes.
- Simetría, por la mediana en el interior de la caja y de la caja dentro de los bigotes.
- Tamaño de las colas, se observa por la amplitud de los bigotes en relación a la caja y por los valores atípicos representados.

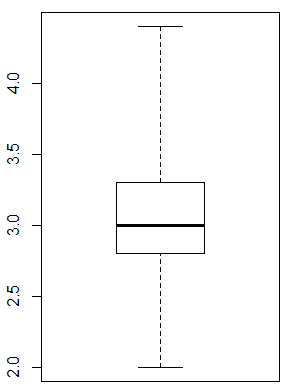
Sin valores atípicos

# Sin valores atípicos
boxplot(iris$Sepal.Width, range = 0)

En el caso de no querer mostrar valores atípicos, especificamos range = 0. Los bigotes se extenderán hasta los extremos de los datos.

Datos

Para obtener los valores de los diferentes elementos del gráfico tenemos varias opciones:

Resumen con los 5 números de Tukey: mínimo, bigote inferior, mediana, bigote superior, máximo

fivenum(iris$Sepal.Width)

[1] 2.0 2.8 3.0 3.3 4.4

Mediante la función summary que proporciona además la media.

summary(iris$Sepal.Width)  

 Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  2.000   2.800   3.000   3.057   3.300   4.400 

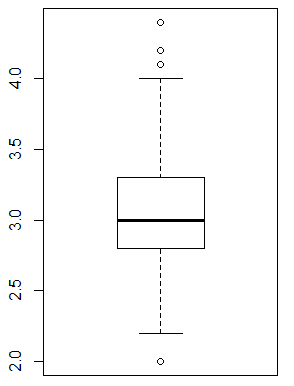
Con valores atípicos

# Con valores atípicos
boxplot(iris$Sepal.Width) 

El cálculo de los bigotes en R se especifica en el argumento range. Por defecto es 1.5, lo que implica:

• Inferior: el mayor de los siguientes dos valores, el mínimo o Q1 - 1,5*RIC.
• Superior: el menor de los siguientes dos valores, el máximo o Q3 + 1,5*RIC.<(li>

Datos

Podríamos emplear las funciones summary y fivenum como hicimos anteriormente, pero los valores de los bigotes serían erróneos pues nos devuelven el mínimo y el máximo. Empleamos la función boxplot.stats que es utilizada por boxplot para producir el gráfico con el cálculo.

boxplot.stats(iris$Sepal.Width)$stats

[1] 2.2 2.8 3.0 3.3 4.0

Si en lugar de 1,5 empleamos otro coeficiente en boxplot, lo especificamos con el argumento coef en boxplot.stats.

boxplot(iris$Sepal.Width, range = 2) 
boxplot.stats(iris$Sepal.Width, coef = 2)$stats 

Orientación y formato

Existen muchas opciones para formatear el gráfico disponibles en la ayuda de la función. A continuación, simplemente lo orientamos horizontalmente, le cambiamos el color y añadimos un título al eje.

boxplot(iris$Sepal.Width,
        col = 'palegreen',
        xlab = "Sepal Width",
        horizontal = TRUE)

Entradas relacionadas

• Diagrama de caja con intervalos de confianza para la mediana
• Diagramas de caja con ggplot2 en R. Una introducción.

Referencias

• Función boxplot
• Box plot
• Diagrama de caja